Mathematics is the science of logical thinking and systematic reasoning. Its references, results and conclusions are based on a definite process of logical thinking and reasoning. Our country has rich tradition in Mathematics. Ancient and medieval Indian mathematical works, all composed in Sanskrit, consisted of a section of sutras in which a set of rules or problems were stated in verse in order to aid memorization. Vedic mathematics, which simplifies arithmetic and algebraic operations, has increasingly found acceptance the world over. Vedic Mathematics helps find solutions in a single or a few steps where as conventional methods require multiple steps. Vedic Mathematics eases and simplifies multiplication, divisibility, complex numbers, squaring, cubing, square and cube roots. Even recurring decimals and auxiliary fractions can be handled by Vedic Mathematics. The basis of Vedic mathematics, are the 16 sutras and the 13 upsutras, which attribute a set of qualities to a number or a group of numbers. A book on Vedic Mathematics was written by Jagadguru Swami Bharati Krishna Tirthaji and first published in 1965. It contains methods for mental calculation claimed to be based on the Parisista of Atharva Veda. Although the book was first published in 1965, Tirthaji had been propagating the techniques since much earlier through lectures and classes.[The mental calculation system mentioned in the book is also known by the “Vedic Mathematics”. However, its characterization as “Vedic” mathematics has been criticized by many academics through many publications and dailies in our country.
Life of Sri Bharati Krishna Tirthaji Maharaja:
The “Vedic” methods of mental calculations in the decimal system are all based on the book Vedic Mathematics by Jagadguru Swami Bharati Krishna Tirthaji Maharaja which appeared in 1965 and which has been reprinted many times. Swami Bharati Krishna Tirthaji Maharaja was born in 1884 near Madras as Venkatraman Shastri. He studied English, Mathematics, Sanskrit, and other subjects at various schools and colleges in India. In 1911 he quit his teaching job in order to devote himself completely to study and meditation in an ashram near Mysore. In 1919 he was initiated as a sannyasi (monk) and received the name Bharati Krishna Tirtha. In 1925, he became a Shankaracharya himself. Swami Bharati Krishna Tirthaji Maharaja travelled extensively through India, and, at the invitation of the Self-Realization Fellowship of Yogananda, also to the United States in 1958. Swami died in 1960. His work on Vedic Mathematics appeared posthumously in 1965 and was reprinted several times.

Vedic Mathematics and the Digital World:
Digital Electronics essentially deals with binary numbers or ‘bits’ in the form of ones and zeros representing digital signals In fact, digital electronic circuits are those circuits that handle digital signals. The subject has become so popularly advanced that we are living in a digital world where many advanced digital system ease our lives. The fundamental building blocks of any digital systems are said to be adders and multipliers, the circuits which perform binary addition and multiplication. The concepts of Vedic Mathematics are now being extensively used by many researchers and academicians in the design of multipliers and other circuits which form fundamental building blocks of digital and Digital Signal Processing (DSP) systems. The principles of Vedic Mathematics are now being considered for the hardware implementation of many Digital Signal Processing algorithms for reasons involving parallelism, efficiency, chip area and speed. Faster additions and multiplications are of extreme importance in DSP for Convolution, Correlation, Discrete Fourier transform (DFT), Digital Filtering and so on. A multiplier is one of the key building blocks in almost every DSP system. The core computing process being a multiplication routine, DSP engineers are constantly looking for new algorithms and their hardware implementation. Such algorithms can be implemented using Hardware Description Languages (HDL) and Field Programmable Gate Array (FPGA) modules.
Vedic Multiplication:
Vedic formulae are based on the natural principles on which the persons mind works and hence expectations are that the use of Vedic mathematics simplifies typical calculations in conventional mathematics. Vedic mathematics is methodology of arithmetic policy that allows more efficient speed performance. It also provides some efficient algorithms, which can be applied to various branches of engineering such as Digital Design, Digital Signal Processing and computing at large. Multiplication can be based on the algorithm called Urdhva Tiryakbhyam (meaning Vertically & Crosswise) found in Vedic Mathematics. Urdhva Tiryakbhyam Sutra is a general multiplication formula applicable to all cases of multiplication

A very important feature of a Vedic multiplier is that generation of partial products and additions can be done concurrently and hence is well adapted to parallel processing. This feature makes a Vedic Multiplier more attractive for binary multiplications. The multiplier offers the advantage that as the number of bits increases, gate delay and area increases very slowly as compared to other multipliers. Vedic Multipliers can become part of a microprocessor. Since the partial products and their sums are calculated in parallel, the multiplier will not depend heavily on the clock frequency of the processor. The processing power of the multiplier can easily be increased by increasing the input and output data bus widths.
(Courtesy: Internet Sources)
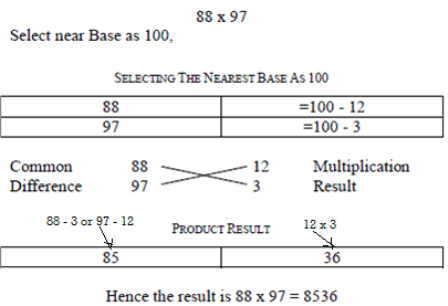
Nikhilam Navatascaramam Dastah (or Nikhilam Sutra) literally means “all from 9 and last from 10”. Nikhilam Sutra is an easier method of multiplication using Vedic Mathematics when numbers are closer to powers or multiples of 10. The method is applicable to all the cases of multiplication but it is more efficient in case of multiplication of large numbers. In this method, the compliment of the large number is found from its nearest base to perform the multiplication operation on it, hence larger the original number, lesser the complexity of the multiplication. Multiplication complexity is further increased when one number is less than its nearest base and the other number is greater than the base and conversion from Vinculum to positive form is required. “Vinculum” is the minus sign put on top of a number. Conversion from Vinculum to positive form is required when the multiplication result is a negative number. This means that further complementation will be required to produce accurate final results.
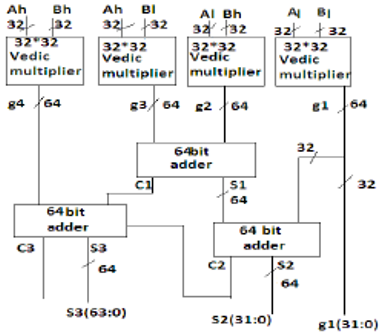
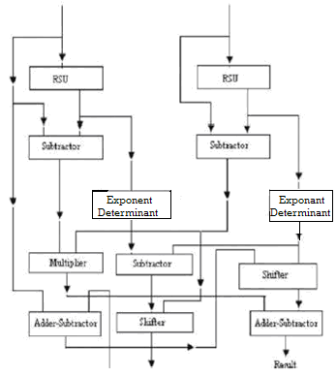
A Vedic Multiplier using Nikhilam Sutra will comprise of blocks such as Radix (Base) Selection Units, Subtractors, Exponent Determinants, Multipliers and Shifters. The Radix Selection Unit (RSU) will select proper radices corresponding to the input numbers while Shifters shift data bits in the desired direction. Adders, Multipliers, Subtractors and Exponent Determinants perform their intended functions.
(Courtesy: Internet Sources)
Circuits to compute the square of a number (squarer) as well as Multiply and Accumulate (MAC) Units can be built using Vedic Multipliers. The advantages of Vedic multiplier like increase in speed, decrease in delay, decrease in power consumption, decrease in area occupied will also apply to such MAC units DSP algorithms like Convolution, Correlation, Discrete Fourier Transform, Fast Fourier Transform etc employ MAC units, which enables efficient computing in terms of speed, delay and complexity
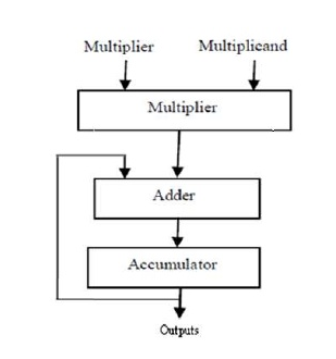
Arithmetic and Logic Units (ALU) based on Vedic Sutras may be of immediate interest to our digital design engineers. ALU is the heart of any processor. The speed of any processor depends on the computational time required to complete any task in the ALU. Again, the speed of an ALU depends on the functioning of its internal blocks. Adders and multipliers being the main fundamental blocks inside the ALU, implementation of efficient and high speed adders and multipliers are necessary to improve the speed and performance of ALU.
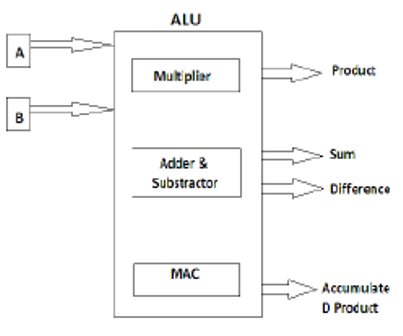
Again, multipliers are the essential building blocks in the hardware implementation of several digital circuits and Digital Signal Processing algorithms such as Frequency Domain Filtering (FIR and IIR filters), Convolution, Correlation, Fast and Discrete Fourier Transforms. The block diagram of a Convolver comprises of multiplexers, multipliers, demultiplexers and adders. Multiplication can be performed using Vedic multipliers to speed up the process.
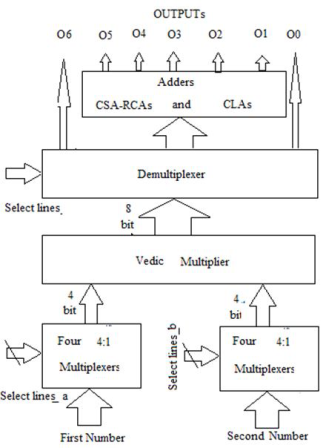
(Courtesy: Internet Sources)
Vedic Mathematics finds potential use in Public Key Cryptography where operations involving exponentiation such as computation of second and higher order powers may be required. Vedic Mathematics when applied to cryptographic encryption and decryption algorithms will help reduce the computation time.
Conclusion:
The demand for high speed processing has been increasing as a result of expanding computer and digital signal processing applications. Higher throughput arithmetic operations are important to achieve the desired performance in many real-time signal and image processing applications. DSP algorithms have found applications in mobile communication and satellite communication systems. Since multiplication and squaring dominates the execution time of most DSP algorithms, there is a need of high speed multiplication and squaring of numbers. Vedic building blocks such as Adders and Multipliers blend tradition with technology and may find extensive use in digital electronics and digital signal processing applications in the near future.
.







