The expanded availability of high speed and very high speed ADCs and digital processing is making oversampling a practical architectural approach for broadband and RF systems.Semiconductor scaling has done much to boost speeds and lower costs (such as in dollars, power, and board areas), enabling the system designer to explore different avenues of converting and processing signals using broadband converters. These techniques change the way we think about signal processing, and the way we specify the products.
This article describes how looking at noise spectral density (NSD), and its distribution over the band of interest, can be insightful and guide the system designer toward the selection of the most appropriate converter.
PROCESSING GAIN: HOW MUCH OF THE NOISE IS IN MY BAND OF INTEREST?
Consider the simplified case shown in Figure 1.We are clocking our ADC at 75MHz, and running an FFT on the output data, so we see a spectrum from dc to 37.5MHz.Our “signal of interest” is the only strong signal present and happens to be located around 2MHz.When the signal-to-noise ratio (SNR) of the data converter is specified, it will indicate the power in a full-scale signal compared to the total noise power present in all the other frequency bins. For white noise (which will include quantization and thermal noise in most situations), the noise is evenly spread across the Nyquist band of the converter; in this case, from dc to 37.5MHz.
If we know where the signal is (in this case, between dc and 4 MHz), we can apply digital post processing to filter out, or throw away everything above 4MHz(keeping only what is in the red box).In this case, we would be throwing away
7/8 of the noise and keeping all of the signal energy—essentially improving our SNR by 9dB.Stated another way: if we know the signal is going to be in one half of the band, we can throw away the other half of the band and eliminate only noise—improving our SNR by 3dB.This leads to a familiar rule of thumb that processing gain can provide
3dB/octave of SNR improvement for oversampled signals in the presences of white noise.In our previous example, we were able to apply this technique across three octaves (a factor of 8), and realize 9dB of SNR improvement.
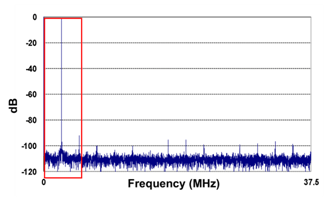
Of course, we realize that if the signal is going to be somewhere between dc and 4MHz, we don’t need 75MSPS to represent the signal:9 MSPS to 10MSPS would meet the Nyquist sampling theorem bandwidth requirements.We can readily decimate the 75 MSPS sample data by 8× to produce an effective 9.375 MSPS data rate while preserving the noise floor in the band of interest.It is important to do the decimation properly—if we decimate simply by throwing away seven out of every eight samples, the noise will fold, or alias, back into our band of interest, and we will not realize any SNR improvement.We must filter, then decimate, in order to realize the processing gain.Note that a perfect brick wall filter would eliminate all the noise and give you the ideal 3dB/octave of processing gain.In practice, the amount of filter stop band rejection you need is a function of how much processing gain you are trying to achieve.
It is very important to recognize that the rule of thumb of “3dB/octave” is based on an assumption that the noise is white.This is a reasonable assumption in many, but by no means all, cases.One important exception is where the dynamic range is limited by nonlinearity or other spurs.In these cases, the “filter and throw away” approach may not catch the performance limiting spur.In the example in Figure 4, we see that the 2ndharmonic spur is the dominant one, and falls inside the red box—so while we realized a 9dB improvement in SNR through processing gain, there was no improvement in SFDR. Later in this paper, we’ll consider the special case of noise shaped converters, where the processing gain can be much greater than 3db/octave.
CONVERTING SNR AND SAMPLE RATE INTO NOISE SPECTRAL DENSITY
The problem gets more interesting where there is more than one signal present in the spectrum; for example, multiple radio stations in the FM band.In terms of recovering any one signal, we recognize that what matters is not the overall noise of the data converter, but the amount of the converter noise that falls into our band of interest:digital filtering and post processing is going to eliminate all the out of
band noise.
This leads us to the observation that there are multiple paths to reduce the amount of noise that falls into the red box.We can use a 75MHz ADC with a better SNR (less noise), or we can use an ADC with the same SNR and clock it faster (say at 150 MHz), thereby spreading the noise over a broader bandwidth, leaving less noise in the red box.Comparing these two cases, we see that two converters with different SNR will provide an equivalent amount of noise in the red box (based on their different sample rates).This raises the question—is there a better specification than SNR for quickly comparing converters to determine the performance you are going to get in the red box?
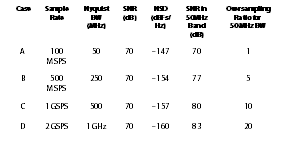
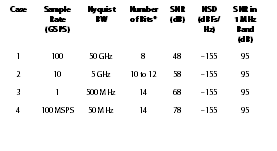
This is where noise spectral density (NSD) comes in.By specifying noise as a spectral density (typically in dB with respect to full scale/Hertz of bandwidth, or dBFs/Hz), we can “normalize” for cases with different ADC sampling rates to determine who might have the lowest noise for our situation of interest. Table 1 examines a data converter with 70 dB of SNR, and illustrates the improvement we see in noise spectral density as we increase the sample rate from 100MHz to 2GHz.Table 2 illustrates several different combinations of SNR and sampling rates for some very different converters, but all have the same NSD, and so each would have the same total noise across a 1MHz channel.In a conventional single carrier system, it might seem absurd to use a 10GSPS converter to capture a 1 MHz signal—but in a multicarrier, software-defined system, that is exactly what you may be doing.The contemporary example is a cable set top box, which may use a 2.7 GSPS to 3 GSPS full spectrum tuner to capture signal coming off of the coax cable in order to recover 6MHz TV channels.
For data converters, noise spectral density will typically be specified in units of dBFS/Hz (dB with respect to full scale per Hz, a relative measure) providing a sort of “output referred” measurement of the noise level—or, alternatively in dBm/Hz (dB-milliwatts/Hz), or even dBmV/Hz (dB-millivolts/Hz) to provide a more absolute measurement, or input referred indication of the data converter’s noise.SNR, full-scale voltage, input impedance, and Nyquist bandwidth can also be used to calculate an effective noise figure for an ADC—a fairly involved calculation that is explained in Reference (MT-006).
THE ADVANTAGES TO OVERSAMPLING
Running an analog-to-digital converter at higher sample rates generally means higher power consumption, both in the ADC itself, and in the subsequent digital processing.Table 1 illustratesthat the oversampling does provide improvement in NSD—but is it worth it?As Table 2 shows, we could also achieve improved NSD by using a lower noise converter.Asystem that needs to capture multiple carriers will need to be running at a higher sample rate, so each carrier is oversampled.However, there are a number of additional benefits to oversampling:
- Simplification of the antialias filtering—the act of sampling will alias higher frequency signals (and noise) back down into the Nyquist band of the converter—to avoid aliasing artifacts, these signals must be suppressed by a filter in front of the ADC.Transition band of the filter is between the highest desired capture frequency FIN, and the alias of that frequency FSAMPLE-FIN.As FIN approaches FSAMPLE/2, the transition band of this antialias filter becomes very narrow, requiring a very high order filter.Oversampling by 2 to 4 substantially relieves this constraint in the analog domain and places the requirement in the relatively easier to process digital domain.
- Minimize the impact of folding converter distortion products. Even if you have a perfect antialias filter, imperfections in the ADC will generate spurs and other distortion products—including some very high order harmonics.These harmonics will also fold across the sampling frequency—potentially falling back in band and limiting our SNR in our band of interest.At higher sample rates, the desired band becomes a small fraction of the Nyquist bandwidth and therefore reduces the folding occurrences.Note: although not discussed here, it is worth mentioning that oversampling also aids in the frequency planning for other system spurious that might fold in band such as other device clock sources.
- Processing gain—as we have noted, we get the
3dB/octave of processing gain on any white noise—this generally includes thermal and quantization noise, but may also include noise from certain types of clock jitter.
As higher converter and digital processing speeds become more readily available, system designers are more frequently using some amount of oversampling to leverage these advantages.
A WORD OF CAUTION REGARDING NOISE FLOORS AND FFTS
One may be tempted to compare converters by inspecting spectral plots and looking at “how far down is the noise floor?”When making such comparisons, it is important to remember that the plotting of the spectrum is dependent on the size of the FFT one runs.Larger FFTs will break the bandwidth into more bins, therefore accumulating less noise in each bin, and the spectral plot will show a lower noise floor.This is just a plotting artifact; the noise spectral density has not changed (this is the signal processing equivalent of changing the resolution bandwidth of a spectrum analyzer).If the sampling rates and FFT sizes are identical (or scaled appropriately), comparing floors is acceptable—otherwise, it can be misleading.Again, the NSD specification provides a useful direct comparison.


WHEN THE NOISE FLOOR IS NOT FLAT—Σ-Δ MODULATORS AND OTHER SPECIAL CASES
Our discussions of processing gain and oversampling so far have been working under the assumption that the noise is flat across the Nyquist band of the converter.That is a reasonable approximation in many cases, but there are a number of situations where that assumption does not hold.We have discussed the fact that processing gain does not really apply to spurs, though oversampled systems may offer some advantages in frequency planning and handling spurs.1/f noise and some types of oscillator phase noise will have spectral shaping, and processing gain calculations will not apply.
One important area where the noise is not flat is the field of Σ-Δ converters.Σ-Δmodulators use feedback around the quantizer to shape the quantization noise of the modulator—lowering the noise that falls into a band of interest at the expense of raising the noise out of band(see Figure 3). One can see that for this kind of shaped noise, the gain from discarding the out-of-band noise can be much greater than the case in Figure 1, and in fact, aΣ-Δmodulator routinely realizes processing gains of 9 dB to 15dB/octave or more for the portion of the noise that is shaped by the modulator(not all noise sources in the system are shaped by the modulator feedback).
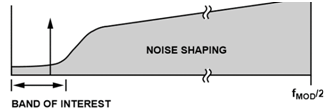
A more detailed treatment of Σ-ΔADCs is beyond the scope of this article, but we can see that that using NSD as the specification for determining the in-band usable dynamic range is particularly helpful for Σ-Δmodulators.Figure 4 shows a zoomed in plot of the noise floor for a high speed bandpass Σ-ΔADC. Across the 75MHz band of interest (with center frequency at 225 MHz), the noise is around
–160dBFS/Hz, providing more than 74dBFS of SNR.

CONCLUSION
The expanded availability of high speed and very high speed ADCs and digital processing is making oversampling a practical architectural approach for broadband and RF systems.Semiconductor scaling has done much to boost speeds and lower costs (for example, in dollars, power, and board areas), enabling the system designer to explore different avenues of converting and processing signals either using broadband converters with flat noise spectral density or band-limited Σ-Δconverters with high dynamic range in the desired band of interest. These sorts of techniques change the way we think about signal processing, and the way we specify the products.In pondering how to capture a signal, engineers may be called upon to compare systems that may operate at very different speeds.Noise spectral density can be considerably more useful than SNR specifications making these sorts of comparisons, or looking at how a software-defined system will handle signals of different bandwidths.It does not replace the other specifications, but is a useful item to add to your spec list.
ACKNOWLEDGEMENTS
The authors would like to thank the many people of the High Speed Converter Group of Analog Devices that contributed to the contents of this article. In particular we would like to thank Allen Barlow, Paul Hendriks, and Anthony DeSimone.
References
Kester, Walt.MT-006ADC Noise Figure—an Often Misinterpreted Specification.Analog Devices, Inc., 2014.






