This article outlines why LTspice is better at yielding correct results than other SPICE implementations.
Analog design engineers lean heavily on simulation to predict circuit performance. The value of a simulator hangs on how well it can predict physical reality, and how quickly it can produce results. Discrepancy between simulated and real performance can send a product into costly iterative debugging cycles.
SPICE is used for analog circuit simulation because it can compute the full large signal behavior of arbitrary circuits. Three numerical methods used in SPICE account for its success in analog circuit simulation. Specifically:
- Newton iteration to find the solution of circuits with nonlinear elements
- Sparse matrix methods to corral huge matrices into the address space of a practical computer
- Implicit integration to integrate the differential equations that arise from circuit reactances
The ability of a SPICE simulator to reliably produce correct results depends on how well these methods are implemented.
Newton Iteration
Newton iteration involves expanding each nonlinear circuit device I-V curve as a Taylor series but keeping only the first two terms and then solving the resultant system of simultaneous linear equations. If the solution of the linear system is indeed the very point about which the Taylor series was expanded, then, because the Taylor approximation is exact at that point and accurate near it, the solution of this linear system is in fact the correct solution to the original nonlinear circuit[i]. Success of convergence of Newton iteration results in finding a numerical proof that the correct solution of your circuit was found.
[i] Otherwise the solution of the linear system is used as an iteration step: The original nonlinear circuit is re-expanded as a new Taylor series about this solution, again keeping only the first two terms, and then solving the resultant system of simultaneous linear equations. The process repeats until the proof that the correct solution has been found is successful.
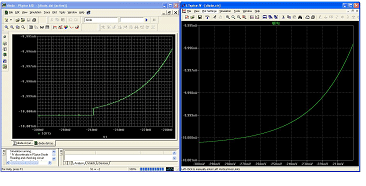
Robustness of Newton iteration depends on (1) having all circuit element I-V curves to be continuous in value and slope and (2) all non-linear elements being bypassed with capacitance so that the previous time step solution is a good starting point for the Newton iteration of the current time point. Conditions (1) and (2) are met by any physical circuit, but SPICE programs usually don’t get this right because the semiconductive devices in Berkeley SPICE have discontinuities and these implementation errors have spilled over to pay-for SPICE implementations. These discontinuities do not occur in LTspice. To illustrate an example, Figure 1 shows the I-V curve of a diode in PSpice[i] verses LTspice. The netlist used in each case is
* I-V discontinuity in PSpice Diode
V1 N001 0 0
D1 N001 0 D
.dc V1 -.3 -.2 2u
.probe
.model D D(Is=10n)
.end
The PSpice diode I-V curve is discontinuous in both value and slope. Such discontinuities exist in most of the semiconductive devices in PSpice but none of the semiconductive devices in LTspice.
Sparse Matrix Methods
The Taylor series is multidimensional—one dimension for each unknown voltage node in the circuit. For an analog IC, this can be 100,000 distinct voltage nodes, leading to a conductivity matrix of 100,000 by 100,000, or 80 billion bytes for double precision matrix coefficients. Even today’s 64-bit processors don’t bond out enough address lines to access that much memory. Fortunately, almost every coefficient is zero, so they don’t need to be stored. Sparse matrix methods keep track of only the nonzero elements. This allows a huge matrix to be solved in a comparatively tiny address space.
The sparsity of the matrix arises from the physical nature of practical circuits. Most nodes are only connected to a few other nodes. For example, even if you write out the conductively matrix of a circuit that looks like a fishnet grid of resistors, the matrix is almost diagonal because each node is resistively connected only to adjacent nodes. Practical circuits aren’t as dense with connections as fishnets are with knots. The sparsity of a large analog circuit is in the parts per million range. This sparsity is what allows the matrix to be solved in a present day computer. Newton iteration of analog circuits is not possible without sparse matrix methods.
The greatest similarity across SPICE implementations is in these sparse matrix methods. All SPICE programs use LU factorization. Most SPICE implementations use a sparse matrix library derived from the code distributed with the academic Berkeley SPICE code, but some, usually marketed as a fast SPICE, try to improve on it by using an enhanced sparse matrix library such as SuperLU[ii].
A better approach is to simply to get the processor to do the math at the theoretical FLOP limit of the underlying hardware. The issue is that it takes longer to get the numerical data to the FPU than it does to actually perform the FLOP.
The FPU pipeline usually runs empty. Ultimately, this is a consequence of the fact that all operating systems use dynamic memory allocation. At the time the simulator is written and compiled, the memory location storing the matrix data isn’t known. At run time the simulator requests memory with function call malloc(), which returns an address at which the simulator is allowed to safely store matrix data. Since it isn’t humanly possible to give each matrix element its own name, arrays are used. This means the simulator asks for fewer, but larger, pieces of memory, and the individual coefficients are indexed off the base address returned by malloc(). All that is known at simulator compile time is the address of the address of the base address off which one indexes to reach the matrix element. Resolving this address at run time and fetching the data pointed to by that address into the FPU takes longer than executing the FLOP itself [iii]. Ideally, the addresses of the data required for a calculation would be known ahead of calculation time so that data can be efficiently fetched and the FPU doesn’t have to wait for it.
LTspice eliminates the overhead in getting the data to the FPU with self-authoring assembly language source written at run time, after matrix memory has been allocated, and the addresses returned from malloc() are known. This late-authored code can resolve concrete matrix element addresses in line with the code so the data can be efficiently loaded, allowing the FPU to operate with the pipeline full once the code is assembled and linked with LTspice’s built-in assembler and linker. LTspice is unique in implementing a self-authoring, self-assembling and self-linking sparse matrix solver. The method performs remarkably better than any other technique.
Implicit Integration
Analog circuit simulation requires numerical integration of differential equations to track the behavior of the capacitances and inductances. This is where one sees some of the largest differences between one SPICE implementation and another: the method(s) available for integrating the differential equations.
Numerical integration involves error. Analog circuit simulation entails integrating the behavior of many time constants. The nature of integrating differential equations that have solutions that look like exp(-const*time) are that the errors will in fact add up to infinity unless a numerical method called implicit integration is used[iv]. Without implicit integration, transient analysis would not be possible in SPICE.
SPICE uses second order integration. Most SPICE implementations follow Berkeley SPICE and provide two forms of second order implicit integration: Gear and trapezoidal (trap)[v]. Trap integration is both faster and more accurate that Gear. But trap integration can give rise to a numerical artifact where the integrated discrete time step solution oscillates time step to time step about the true continuous-time behavior. This can cause the user to be suspicious of the correctness of the simulator even though each trapezoid contains the correct integrated area.
Trap ringing has been feared to be so unacceptable to analog circuit designers [vi] that trap integration has been eliminated from one commercial SPICE implementation, PSpice, leaving the slower and less accurate Gear integration as the only available option.
But Gear integration doesn’t just dampen numerical ringing, it dampens all ringing, even physical ringing, making it possible for a circuit that malfunctions in real life, due to an oscillation, to simulate as perfectly stable and functional because the instability was damped out of numerical existence. This has lead to disastrous situations where an IC design is simulated in PSpice, laid out, and fabricated only to find that the circuit doesn’t function due to an instability that PSpice’s Gear integration missed. A mask revision cycle—at considerable expense in time and treasure—is required to remove the instability to try to achieve initial functionality.
In principle, Gear integration error could be reduced by having the IC designer stipulate a small maximum time step. But this is not a viable solution because (1) small time steps slow simulation speed to a crawl and (2) there’s no way to ensure that the time step is small enough anyway.
PSpice’s documentation states that it uses a modified Gear method and does indeed seem better at picking a small enough time step to reduce the error than the Gear integration implementation in Berkeley SPICE.
But PSpice’s method often fails. It is easy to compose a trivial circuit and see the PSpice numerically integrated result deviate dramatically from the true solution than can be found by inspection. Consider Figure 2, which shows a parallel tank circuit with a parallel piecewise linear current source. The current source asserts a spike of current over the first 0.2 ms and is zero thereafter. The solution should be that the tank circuit resonance is excited by the spike of current and thereafter ring at constant amplitude. The netlist of the circuit is given by
* Gear (PSpice) integration error
L1 N001 0 50m
I1 0 N001 PWL(0 0 .1m .1 .2m 0)
C1 N001 0 .1u
.tran 1 1 0 50u
.probe
.end
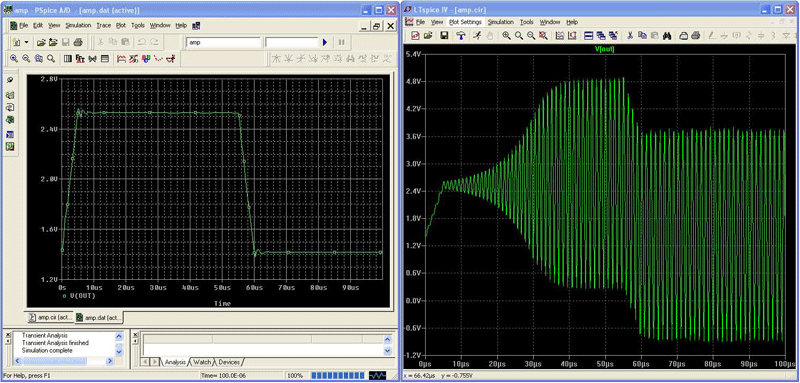
Figure 3 shows that PSpice’s modified Gear integration artificially dampens the ringing, whereas LTspice immediately yields the correct solution. The error in PSpice can be reduced by stipulating a smaller maximum time step (fourth number in the .tran statement). This should be a simple circuit for PSpice’s modified Gear to figure out. But a circuit with many different time constants is basically impossible for PSpice to solve reliably without the engineer manually inspecting how the “solution” converges as one stipulates ever smaller maximum time steps.
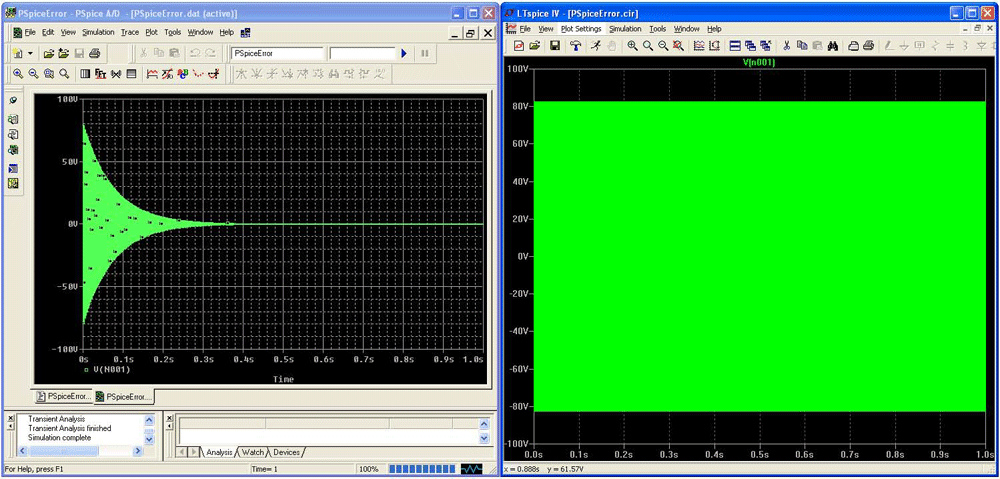
Figure 2 shows PSpice Gear integration clearly doesn’t correctly integrate the two reactances of a trivial circuit with only one node. The nature of the error of Gear integration is to make circuits look more stable in simulation than they actually are in real life. To put the consequences of this error in the perspective of a practical example, Figure 4 shows an audio power amplifier that isn’t stable because compensation capacitor C2 is too small.
PSpice incorrectly simulates this circuit as stable, whereas LTspice gives the correct result. The netlist used in each case is
* Unstable Power Amplifier
Q5 N001 N006 N007 0 Q3904
Q7 N001 N007 OUT 0 Q2219A
Q8 OUT N013 N014 0 Q2219A
Q6 N013 N012 OUT 0 Q3906
V1 N001 0 10
V2 N014 0 -10
R11 N012 N014 5K
R14 OUT 0 8
R9 N006 N008 2K
R10 N008 N012 1K
Q4 N006 N008 N012 0 Q3904
Q1 N005 N009 N011 0 Q3904
Q2 N002 N010 N011 0 Q3904
R3 N011 N014 1K
Q3 N006 N004 N003 0 Q3906
R6 N010 0 20K
R7 OUT N010 200K
V3 IN 0 pulse(0 .1 0 5u 5u 50u 100u)
R8 N001 N003 100
R4 N004 N005 10K
C2 N006 N004 10p
R13 N013 N014 1K
R12 N007 OUT 1K
C3 N006 N012 .001u
Q9 N005 N002 N001 0 Q3906
Q10 N002 N002 N001 0 Q3906
R2 IN N009 9.09K
.tran 100u 100u
.model Q3904 NPN(Is=1E-14 Vaf=100 Bf=300 Ikf=0.4 Xtb=1.5
+ Br=4 Cjc=4p Cje=8p Rb=20 Rc=0.1 Re=0.1 Tr=250n Tf=.35n
+ Itf=1 Vtf=2 Xtf=3)
.model Q3906 PNP(Is=1E-14 Vaf=100 Bf=200 Ikf=0.4 Xtb=1.5
+ Br=4 Cjc=4.5p Cje=10p Rb=20 Rc=0.1 Re=0.1 Tr=250n
+ Tf=.35n Itf=1 Vtf=2 Xtf=3)
.model Q2219A NPN(Is=14.34f Xti=3 Eg=1.11 Vaf=74.03
+ Bf=255.9 Ne=1.307 Ise=14.34f Ikf=.2847 Xtb=1.5
+ Br=6.092 Nc=2 Isc=0 Ikr=0 Rc=1 Cjc=7.306p Mjc=.3416
+ Vjc=.75 Fc=.5 Cje=22.01p Mje=.377 Vje=.75 Tr=46.91n
+ Tf=411.1p Itf=.6 Vtf=1.7 Xtf=3 Rb=10)
.probe
.end
Figure 5 compares PSpice’s erroneously stable result (left) with the correct, oscillating result from LTspice (right). The simulation is a large signal transient. If a small enough time step is stipulated in the PSpice simulation, you can force it to approach the correct LTspice solution, suggesting that PSpice is interpreting the device equations of the transistors correctly, PSpice just isn’t accurately integrating the differential equations.
What is needed is a method with the speed and accuracy of trap but without the ringing artifact. To this quest, whereas PSpice eliminated trap ringing by using Gear integration but tries to pick a good time step, another approach is to use a de-tuned version of trap integration so that it will damp trap ringing but only introduce a hopefully acceptably small error in the true circuit behavior. It is actually possible, but not recommended, to de-tune LTspice’s trap integration with the undocumented option called trapdamp, by adding the SPICE directive
.options trapdamp=.01
to your schematic. You might be able to find a value of trapdamp that duplicates the integration behavior of HSPICE[i]. Nevertheless, I do not recommend using this option because it dampens real circuit behavior and it isn’t necessary in LTspice, which uses a better method of eliminating trap ringing.
LTspice uses an integration method, modified trap, that has the speed and accuracy of trap but without the ringing artifact. Modified trap is a method I invented some years ago and was widely available first in LTspice. To the best of my knowledge, it is the best means to integrate the differential equations of an analog circuit and is not duplicated in any other SPICE program. It is the only method I recommend for circuit design. LTspice does also support the use of the other known methods, trap and Gear, but simply so that a user can duplicate the erroneous results from other SPICE simulators, to verify that the models are interpreted the same and only the integration method is different.
Modified trap is used by LTspice to produce Figure 3. Note that there is no change in ringing amplitude even after it rings for thousands of cycles. This demonstrates that LTspice modified trap does not introduce artificial numerical damping. Modified trap is also used by LTspice to produce Figure 5, where LTspice correctly exposes the amplifier’s instablity.
To demonstrate the ability of LTspice modified trap to eliminate trap ringing, we need a circuit that is prone to trap ringing. Trap ringing is initiated when discrete time step second order integration has trouble representing the exact continuous-time circuit behavior. It can be reduced or eliminated with judicious use of time step and integration order control.
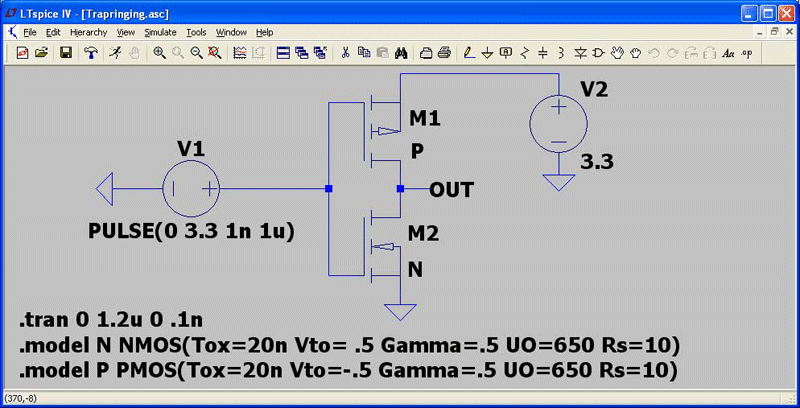
Since LTspice has been the most popular SPICE program for the last 10 years[i], it has seen a lot of circuits and there is a lot of knowledge libraried into the solver to avoid trap ringing, so one has to work a little to find a counter example. Figure 6 shows a circuit that causes trap ringing due to the highly nonlinear capacitance of the gates of an unusually dimensioned MOSFET inverter. Trap ringing is visible in the gate current drive, I(V1).
[i] LTspice is downloaded four times per minute and is the topic of the largest users’ group of any simulator. Using distribution and use figures of other SPICE implementations based on private communication with representatives from the respective companies that sell those other SPICE programs, LTspice is distributed and used three orders of magnitude more than any other SPICE program.
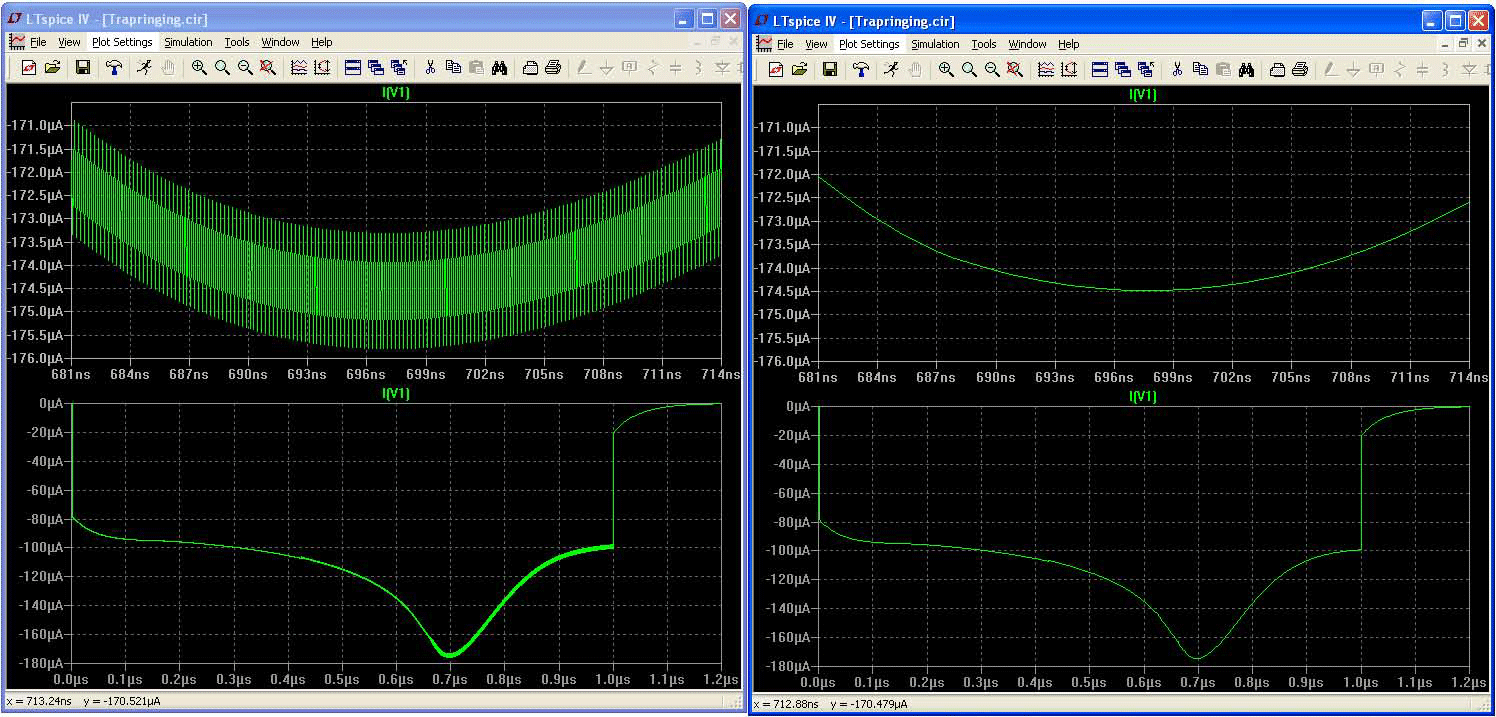
Figure 7 compares trap integration to LTspice modified trap. The top plot shows a zoomed in region of the bottom plot to clearly show the ringing. If you would like to reproduce this result in LTspice, go to the SPICE pane of the Control Panel and select trapezoidal integration instead of the default, modified trap.
The netlist for this simulation is:
* Trap Ringing Example
V2 N001 0 3.3
V1 N002 0 PULSE(0 3.3 1n 1u)
M1 OUT N002 N001 N001 P
M2 OUT N002 0 0 N
.tran 0 1.2u 0 .1n
.model N NMOS(Tox=20n Vto= .5 Gamma=.5 UO=650 Rs=10)
.model P PMOS(Tox=20n Vto=-.5 Gamma=.5 UO=650 Rs=10)
.probe
.end
Note that most SPICE programs won’t run this deck as intended because most SPICE programs use the Meyer capacitance model for this type of MOSFET. Because the Meyer capacitance model doesn’t conserve charge and is inaccurate for short channels, it fell into obsolescence in the 1990s.
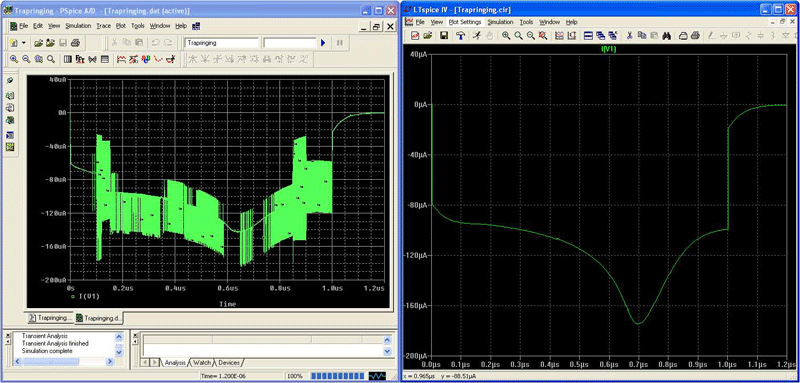
Both LTspice and PSpice have replaced the Meyer capacitance model with the Yang-Chatterjee charge model. Since both simulators use the same updated charge storage equations, they should give the same results. But when we compare the PSpice simulation to LTspice, as shown in Figure 8, PSpice shows remarkably erroneous results. The oscillations visible in the PSpice simulation, though, are not trap ringing because the oscillation isn’t from time step to time step and PSpice doesn’t use trap. This artifact is almost certainly due to an error in differentiating the Yang-Chatterjee charge equations to capacitances in the PSpice Yang-Chatterjee charge model implementation.
Summary
LTspice was not the first SPICE implementation, nor is it the only free SPICE, but it is the best and most widely used SPICE implementation.
Newton iteration, sparse matrix methods, and implicit integration are the core numerical methods of SPICE. The simulator’s robustness, speed and integrity hinge on well these methods are implemented. In the end, a SPICE simulator needs to earn designers’ confidence that it can correctly solve for circuit behavior. This is impossible if the solver doesn’t perform the core numerical methods correctly. LTspice performs these methods correctly and better than any other SPICE implementation.
[i] PSpice is a Cadence trademark. Version 9.2 was used for the screen shots.
[ii] The sparser the matrix, the more closely it can be written as a diagonal, i.e. solved, matrix. Since analog circuit matrices are so sparse, improving LU factorization with SuperLU does not give as much speed advantage as one might hope.
[iii] Eliminating the unknowns of a matrix involves mostly addition, subtraction and multiplication. These instructions cost only three latent clock cycles (There are also some divisions which cost much more than three clocks, but there’s only one division per unknown to be eliminated). Fetching data that is only known by the address of the address of the base address off which one indexes takes much longer than three clock cycles.
[iv] Literature on this points out the numerical solution is not singular if a small enough time step is guaranteed, but in practice, an approach with explicit integration and limited time step size doesn’t work unless you can numerically integrate with infinite precision. The error doesn’t add up to infinity because of round off error but because of approximating the derivative with sampled finite differences. There are no successful general analog circuit simulators that use explicit integration.
[v] SPICE occasionally drops to first order integration. E.g., if an event with a known discontinuous first order time derivative occurs, such as at the transition between two straight line segments of a piecewise linear or pulse function of an independent voltage or current source, most SPICE implementations drop to first order integration for that circuit’s reactances at the transition. The first order version of Gear and trap are both backward Euler.
[vi] Some users are predisposed to be suspicious of SPICE because of popular literature denigrating the value of SPICE simulation.






